第十五章 数学实验室(一)——数字游戏
“数学实验室”听起来有些奇怪,学校里有物理、化学及生物等实验室,但从来没听说有数学实验室,它在哪里?里面有什么?如何去做一个数学实验?这正是在接下来的两章里,我想展示给读者的内容,如何利用编程来解决数学问题,或学习数学知识。
本章中的几个例子,需要读者具备小学数学基础,其实,这里解决的不是数学问题,而是如何把数学问题转变为程序问题,并使用程序语言来解决问题。
数学这门课贯穿了我们整个的学生时代,从小学、初中、高中直到大学,没有哪门课与我们相伴如此之久,因此,数学的烙印深深地刻在我们心里。还记得班里那些数学拔尖的同学吗?当你还没有读懂题目的时候,他们已经把题解出来了,让你的自信心备受打击!在数学这门课中,解题思路之独特(或者说怪异)、解题速度之迅捷,一直备受推崇。然而,凡事都有两个方面,当我们试图将数学问题转化为程序问题时,这种独特和迅捷却成为一种障碍,相反,我们需要让自己的思路慢下来,再慢下来,同时,还要让自己“笨”一点,再“笨”一点。
慢下来,从另一种角度理解,就是把时间放大,好像把“时间”放在一台显微镜下。假设我们平时用1秒钟为时间间隔,来观察事物的变化,又假设“时间”显微镜的放大倍数是1000倍,那么我们将观察到1毫秒的时间间隔内事物发生的变化,这是人类探索“微观”世界的方法,也恰恰是利用计算机解决问题时,所应采用的方法。
所谓“笨”一点,就是让我们退回到蒙昧状态,退回到学龄前,忘记自己学过的数学知识、解题方法与技巧,以最本初的心去寻找问题的答案。
下面我们将以“鸡兔同笼”问题为例,来说明如何将数学问题转化为程序问题,并理解“慢”与“笨”对于我们解决类似问题的意义。
第一节 鸡兔同笼解法之一——手动枚举法
鸡兔同笼问题是一个尽人皆知的经典数学题,题目来自南北朝时期的数学著作《孙子算经》,内容如下: 今有雉兔同笼, 上有三十五头, 下有九十四足, 问雉兔各几何?
“雉”读作zhì,是一种野生的鸟,长着漂亮的羽毛和长长的尾羽,能短距离飞行,俗称野鸡,在北方的冬天,是人们捕猎的目标之一。不过对于我们来说,它最重要的特性是长着两只脚!
你可以列出等式或方程,来解决这一问题,这些方法要么属于算术方法,要么属于代数方法,不过我们这里要给出的是实验的方法,看看我们如何来做这个实验。为了完成这一实验,需要创建一个App Inventor项目,名称为“鸡兔同笼”,下面介绍项目的开发过程。
一、功能说明
- 手机屏幕上显示鸡兔同笼的题目,初始状态下兔数为35,鸡数为0,头数之和为35,足数之和为140,如图15- 1所示;
- 屏幕中部左侧的按钮显示兔子图片,点击该按钮可以增加兔数;右侧的按钮显示鸡的图片,点击该按钮可以增加鸡数;鸡数与兔数之和始终为35;
- 每次点击按钮改变鸡数或兔数时,在屏幕下方显示鸡兔的足数之和;
- 如果足数之和恰好等于题目中给定的数量(94),则播放一段声音,提示用户实验成功。
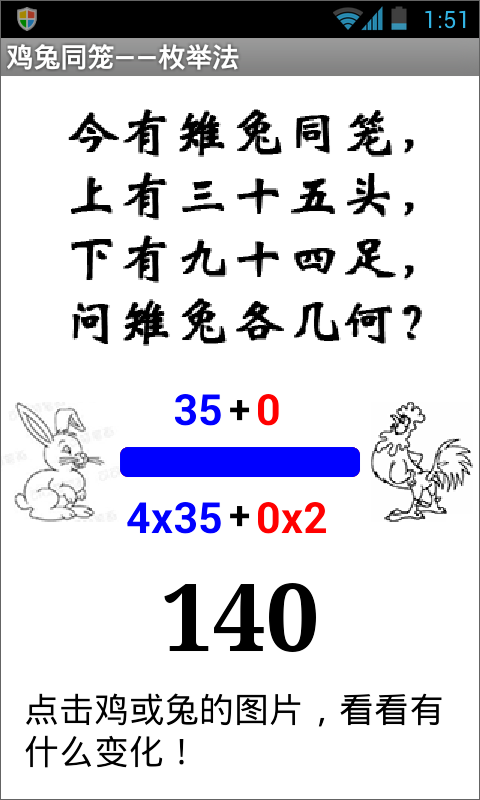 图15-1 鸡兔同笼项目的用户界面
图15-1 鸡兔同笼项目的用户界面二、用户界面设计
1、组件设置
如图15- 2所示,用户界面的上方用一个图片组件来显示题目内容(图片制作在Photoshop中完成),屏幕中部是操作区,用户点击鸡或兔的图片(设置了背景图片的按钮组件),可以增加鸡或兔的数量;用数字滑动条的滑块位置来表示鸡、兔之间数量的比例,同时用标签来显示鸡兔的数量以及鸡兔的足数之和。界面组件的详细设置见表15- 1。
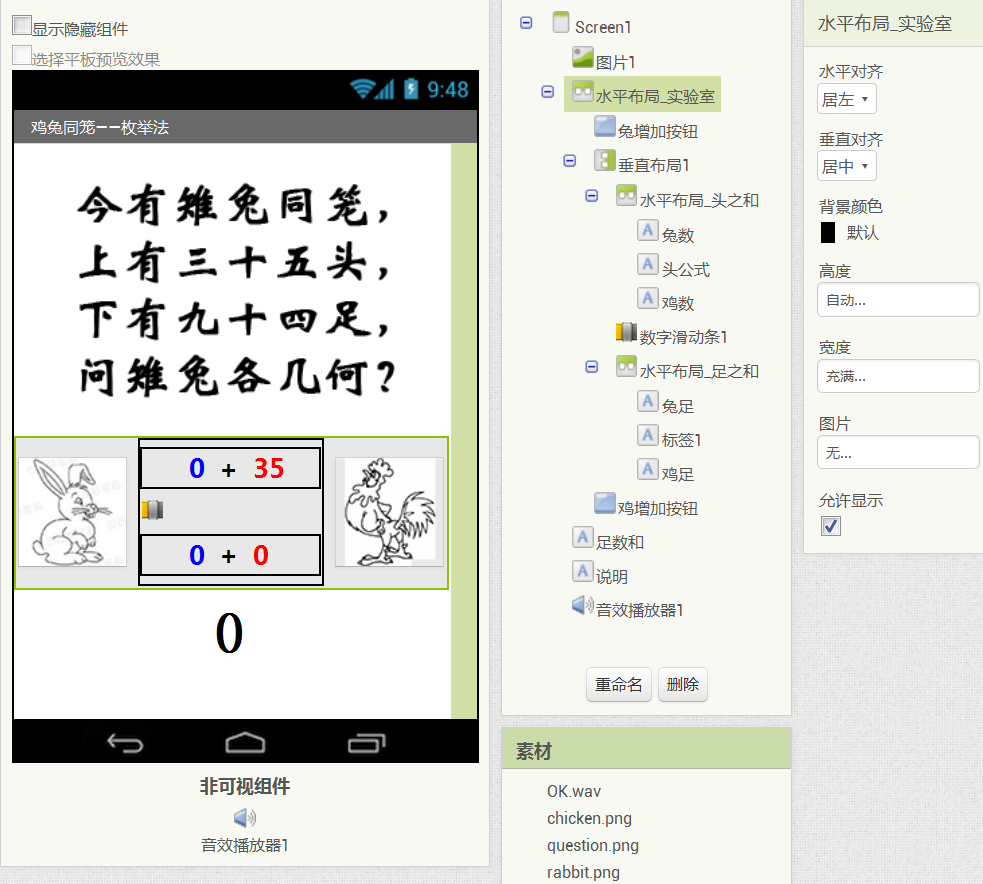 图15-2 解决鸡兔同笼问题的数学实验室——用户界面设计
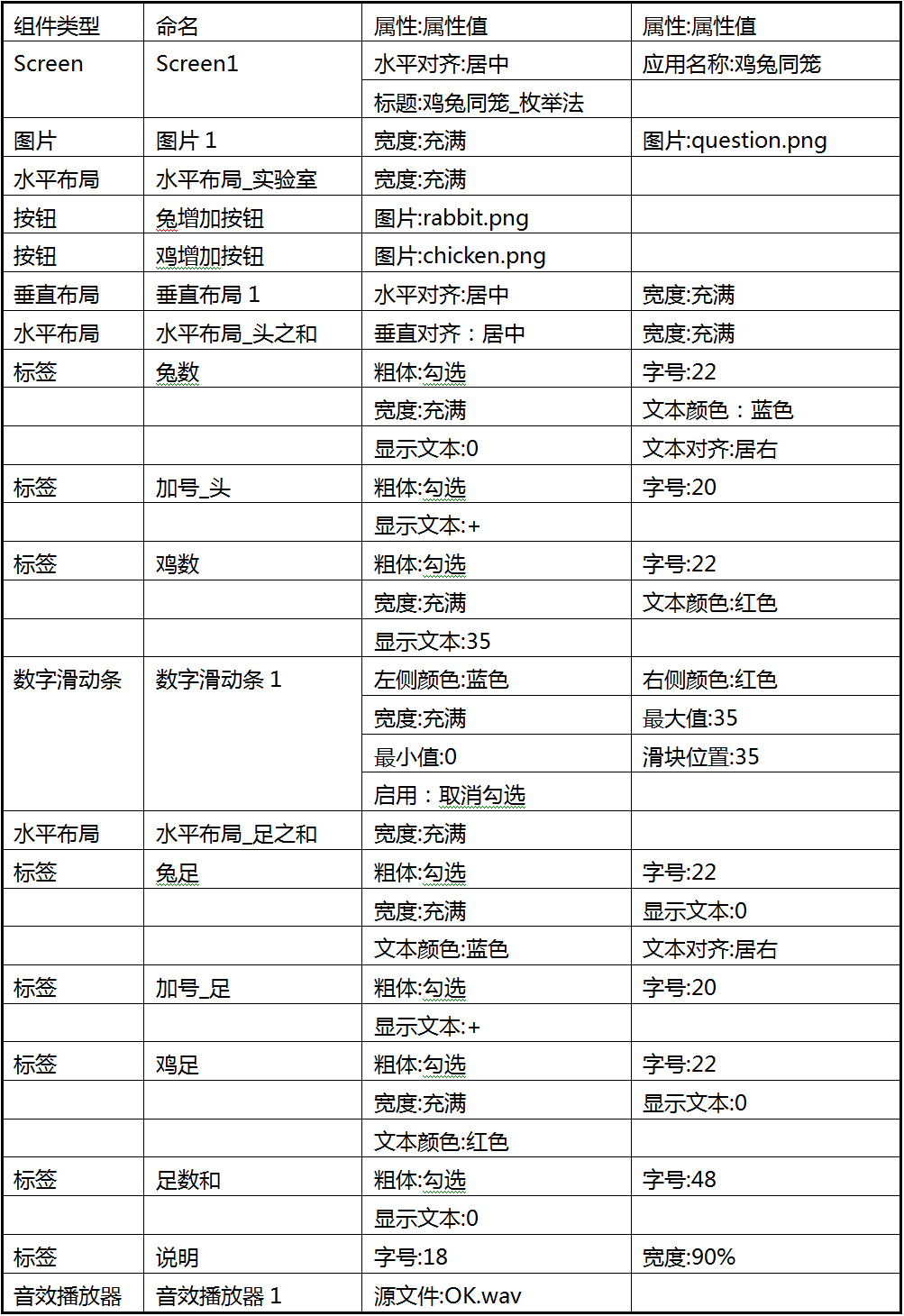
图15-2 解决鸡兔同笼问题的数学实验室——用户界面设计表15- 1 鸡兔同笼项目中组件的命名及属性设置
2、素材规格
如图15- 3所示,准备好素材文件(注意:文件名必须以英文字母、数字及下划线组成),将文件上传到项目中,并设置相关组件的属性(见表15- 1)。
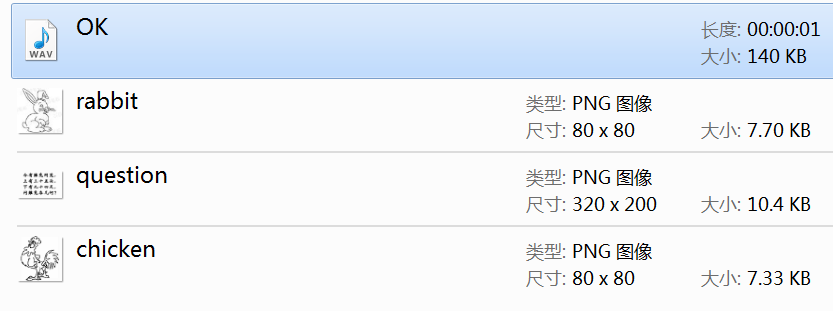 图15-3 项目中素材文件的规格
图15-3 项目中素材文件的规格三、页面逻辑
- 屏幕初始化时,让兔数为35,鸡数为0,并计算该数量比例下鸡兔的足数之和;
- 数字滑动条的滑块两侧颜色不同,颜色条的长度表示数量的多少,左侧为蓝色,表示兔的数量,右侧为红色,表示鸡的数量;屏幕初始化时,滑块位于最右方,整个滑动条均为蓝色(兔数=35);
- 点击兔增加按钮时,兔的数量加1,鸡的数量减1;点击鸡增加按钮时,鸡的数量加1,兔的数量减1;当兔数=35时,兔增加按钮不可用,当鸡数=35时,鸡增加按钮不可用,除此之外,两个按钮同时可用;
- 每次点击兔增加按钮或鸡增加按钮时,都要计算当前鸡兔的足数之和,并用标签显示出来;
- 当足数之和=94时,让音效播放器播放音效。
四、编写代码
1、创建过程——有返回值过程
如图15- 4所示,根据标签上显示的兔数及鸡数,计算兔与鸡的足数之和。
 图15-4 过程——足数之和
图15-4 过程——足数之和2、创建过程——无返回值过程
如图15- 5所示,显示足数过程分别显示了足数的计算方法以及计算结果。
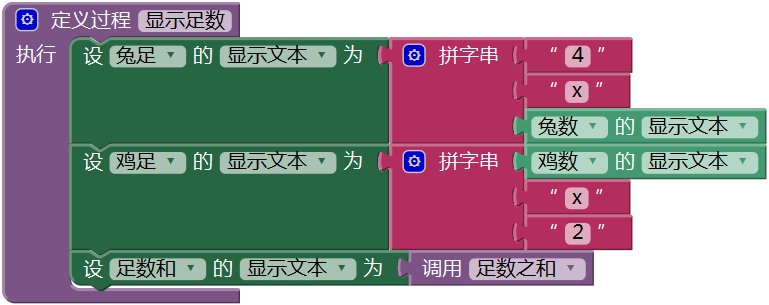 图15-5 过程——显示足数
图15-5 过程——显示足数3、屏幕初始化程序
根据页面逻辑的描述,屏幕初始化时,设兔数=35,由此计算出鸡数,进而求出鸡兔的足数之和,并显示在屏幕上,代码如图15- 6所示。
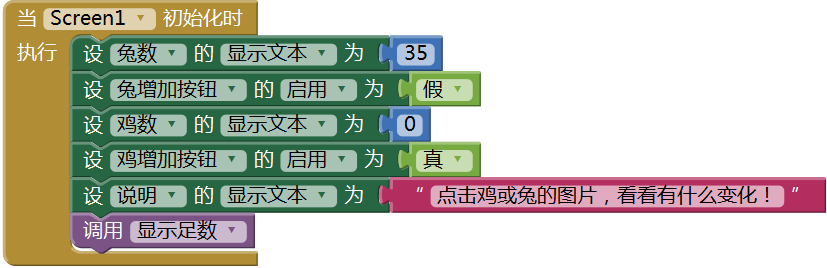 图15-6 屏幕初始化程序
图15-6 屏幕初始化程序4、鸡、兔增加程序
当点击“鸡增加按钮”时,鸡数+1,兔数-1,首先更新鸡数、兔数标签,再更新数字滑动条的滑块位置(向左移动以增加红色条的长度),并显示鸡兔的足数之和;对足数之和进行判断:当足数之和=94时,让音效播放器播放声音,通知用户问题的答案已经找到(也可以用文字的方式通知用户);最后判断鸡数是否为35,来决定是否禁用鸡增加按钮,代码如图15- 7所示。
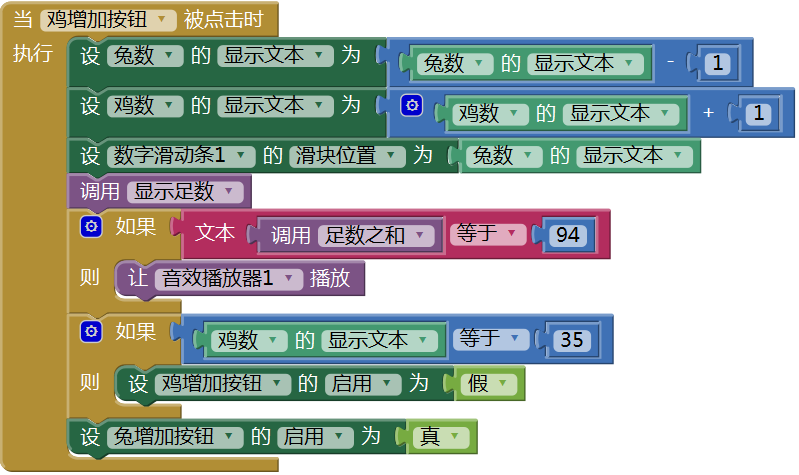 图15-7 鸡增加按钮的点击程序
图15-7 鸡增加按钮的点击程序同样的思路编写兔增加按钮的点击程序,代码如图15- 8所示。
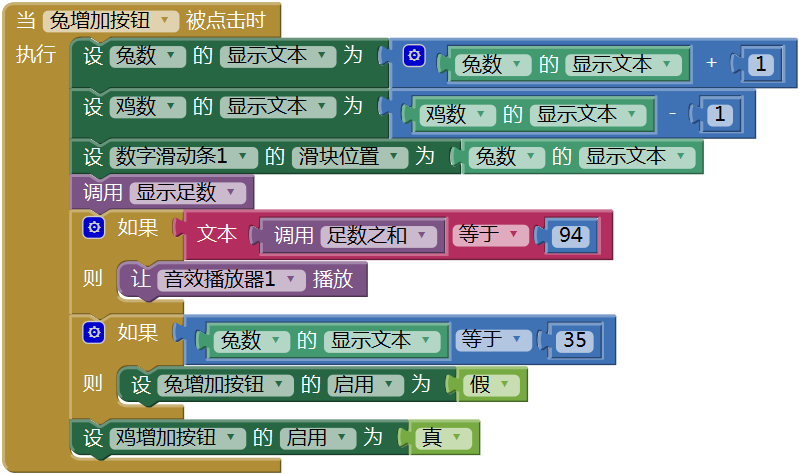 图15-8 兔增加按钮的点击程序
图15-8 兔增加按钮的点击程序五、测试
如图15- 9所示,左一图是屏幕初始化时的鸡兔数量及足数之和,此时兔增加按钮不可用;点击鸡增加按钮,兔数-1,鸡数+1,足数之和也随之改变;当鸡数=23时,听到了音效声,此时足数之和为94,正是题目中给出的数字;继续点击鸡增加按钮,直到鸡数=35,此时鸡增加按钮不可用。
 图15-9 测试结果
图15-9 测试结果六、讨论
所谓手动枚举法,就是手工增加鸡或兔的数量,遍历所有可能的鸡数与兔数,并求出每一种数量下鸡兔的足数之和,从而找到足数之和为94时鸡兔的数量。这是不是一种很“笨”而且很“慢”的方法呢?坦白地讲,这是我第一次遇到这个问题时的想法,但我羞于在课堂上把这个想法讲出来,因为它不够机智,我担心自己被贴上“愚钝”的标签。多年之后,当我试图在讲台上用鸡兔同笼这个例子讲解编程方法时,当初这个“愚钝”的想法却帮助我顺利地找到了答案。
之所以这种“笨”办法能够奏效,是因为计算机本身恰好也足够的“笨”。计算机的优势在于做简单的事情,并不断重复。由于它的运算速度非常快,对于1GHz的CPU来说,每秒钟的运算次数为109次,因此对于像鸡兔同笼这样的问题,每改变一次鸡兔数量比例,计算一次足数之和,最多只有35次运算,相对于计算机巨大的运算能力来说,这点小小的运算量简直不值一提。
在手动枚举法中,我们通过点击按钮手工增加鸡或兔的数量,每次的增量为1,这件事恰好也是编程语言中循环语句最擅长做的事情,因此不妨将这个单调重复的任务交给机器去完成,这正是我们下一节的目标。
第二节 鸡兔同笼解法之二——程序枚举法
我们在上一节的基础上,对程序稍加修改,就可以很容易地获得问题的答案。在项目中添加一个加速度传感器,利用传感器的摇晃事件,来触发求解运算。为了提示用户操作方法,先修改屏幕初始化程序,代码如图15- 10所示。
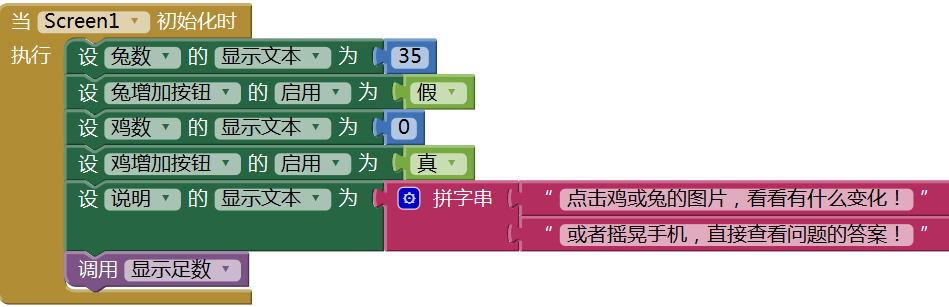 图15-10 修改屏幕初始化程序,提示用户应用的操作方法
图15-10 修改屏幕初始化程序,提示用户应用的操作方法然后,在加速度传感器的摇晃事件处理程序中,利用循环语句为问题求解,代码如图15- 11所示。当足数之和=94时,利用“说明”标签来显示求解的结果,并播放音效提示用户,测试结果如图15- 12所示。
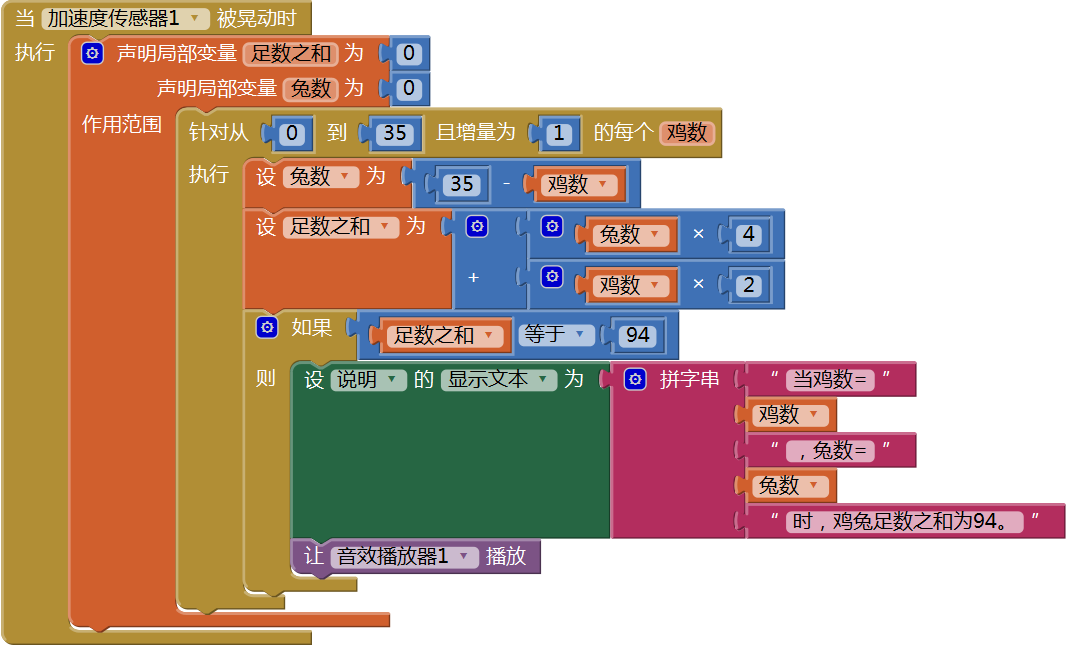 图15-11 用循环语句替代手工改变鸡的数量
图15-11 用循环语句替代手工改变鸡的数量 图15-12 测试结果——用循环语句求解
图15-12 测试结果——用循环语句求解鸡兔同笼问题还可以转变为一个出题的应用,例如,提供两个文本输入框,分别输入鸡数与兔数,程序将自动算出头数与足数之和,出题人可以隐藏鸡兔的数量,只给出头数及足数之和,这样可以生成任意多道不同的题目。
此外,也可以任意给定头数及足数之和,来判断问题是否可解。
这个例子可以帮助我们理解计算机的工作方式,以及用程序来解决实际问题的思路,熟悉循环语句的运行过程及使用方法。读者不妨找来其他类型的应用题,尝试用程序来解决它。
第三节 素数问题求解
一、N是否为素数
素数也称为质数,是只能被1及其自身整除的自然数。对于一个给定的自然数N,如何判断它是不是素数呢?有了之前解决鸡兔同笼问题的“愚钝”思路,这个问题似乎并不难:利用循环语句进行遍历,循环变量的取值从2到N-1,如果N能够被其中的任何一个循环变量整除,则N就不是素数。那么如何判断“整除”呢?所谓“整除”就两个数相除的余数为零,在App Inventor中有一个求余数的块可供使用。
创建一个新项目“素数求解”,用户界面很简单,一个文本输入框,一个按钮和一个标签。如图15- 13所示。设Screen1的标题为“素数求解”,勾选文本输入框的“仅限数字”属性。
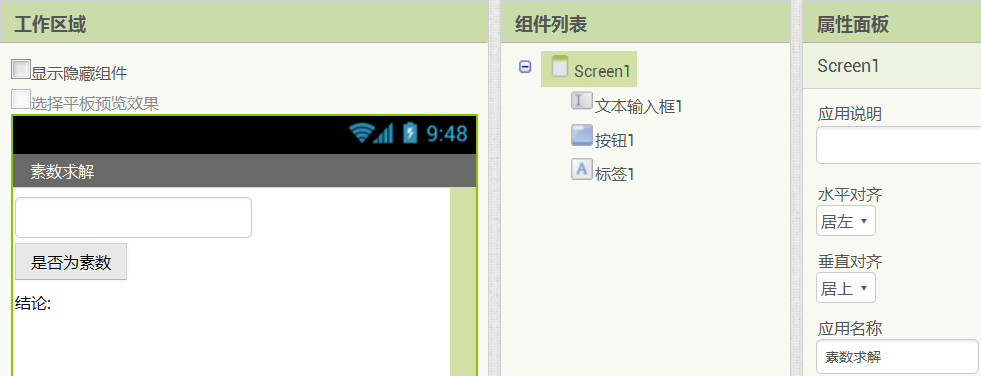 图15-13 新建一个项目——素数求解
图15-13 新建一个项目——素数求解用户在文本输入框中输入一个数字,并点击按钮1;在按钮1的点击程序中,对问题进行求解,并将结果显示在标签中。代码如图15- 14所示,测试结果如图15- 15所示。
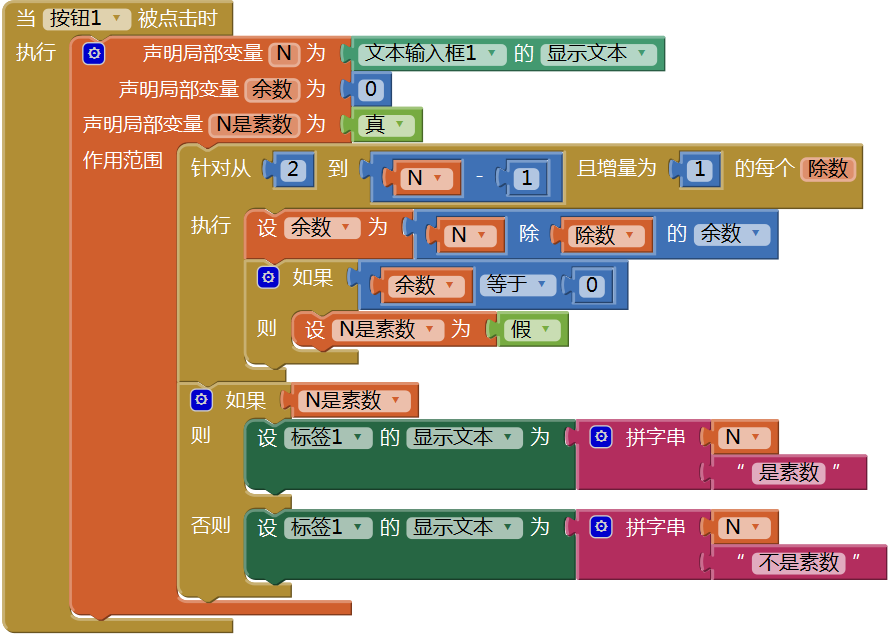 图15-14 判断一个数是否为素数
图15-14 判断一个数是否为素数 图15-15 测试——对于输入的任意自然数,判断其是否为素数
图15-15 测试——对于输入的任意自然数,判断其是否为素数二、算法的改进
你会发现,随着数字的变大,运算所需的时间变长。被判断的数字每增加1,将增加一次循环,也就是增加一次求余数运算,并增加一次余数是否为零的判断,判断数字33133时共进行了33131次求余运算,外加33131次余数是否为零的判断,因此,等了好一会儿结果才显示出来。
是否可以通过改进算法,来提高计算速度呢?答案是肯定的。这时候我们需要动用人类的智慧,来帮助电脑提高工作效率。
与素数相对应的是合数,合数可以被分解为若干个素数的乘积,这些素数称为这个合数的质因数(素因数)。我们来观察一下60以内的合数,看看它们的质因数有什么特点,如表15- 2所示。
表15- 2 60以内的合数以及它们的质因数
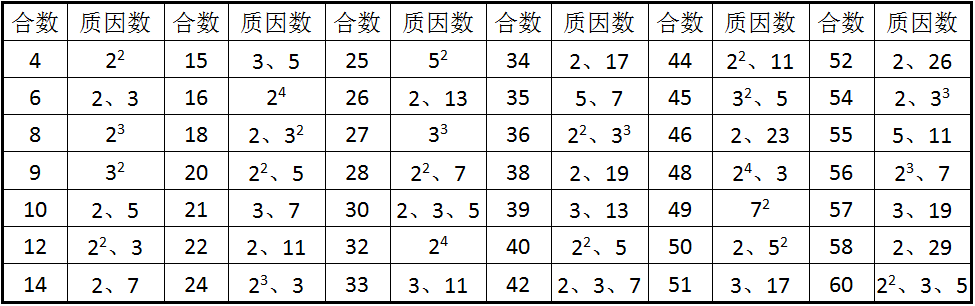
我们来比较某个合数N的最小质因数与N的平方根(√N)之间的关系。我们发现所有合数的最小质因数均小于或等于它的平方根,这条结论也可以换一种说法:对于任意给定的合数N,设P=√N,一定存在一个质数M1,它是N的质因数,且M1<P。
如果这个结论成立,那么我们在判断一个数是否为素数的程序中,循环变量的上限就可以用√N代替N-1,这样就可以减少循环次数。以33133为例,√33131 = 182(就低取整),按照上述结论,循环变量的上限为182,循环次数将减少33131-182=32948次,这将大大缩短计算时间。我们将直接使用这一结论,并在附录中给出该结论的简短证明。下面改造图15- 14中的按钮点击程序,创建一个有返回值的过程——N是素数,并在按钮点击程序中调用该过程。修改后的代码如图15- 16所示。
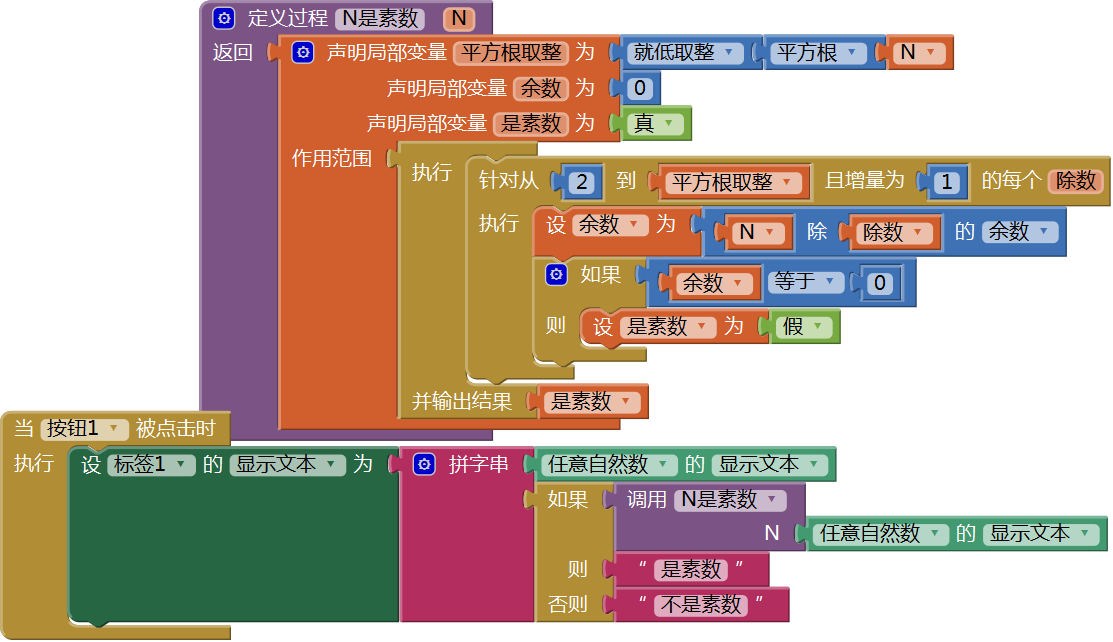 图15-16 将循环变量上限替换为N的平方根取整
图15-16 将循环变量上限替换为N的平方根取整有兴趣的读者可以利用计时器组件,粗略地测量出这两种算法的运算耗时,并进行比较。
三、求N以内的素数
利用“N是素数”过程,可以求N以内的所有素数。创建有返回值过程“N以内的素数”,在设计视图中添加一个按钮组件(按钮2),并在按钮2的点击程序中调用该过程,代码如图15- 17所示,测试结果如图15- 18所示(750以内的全部素数)。
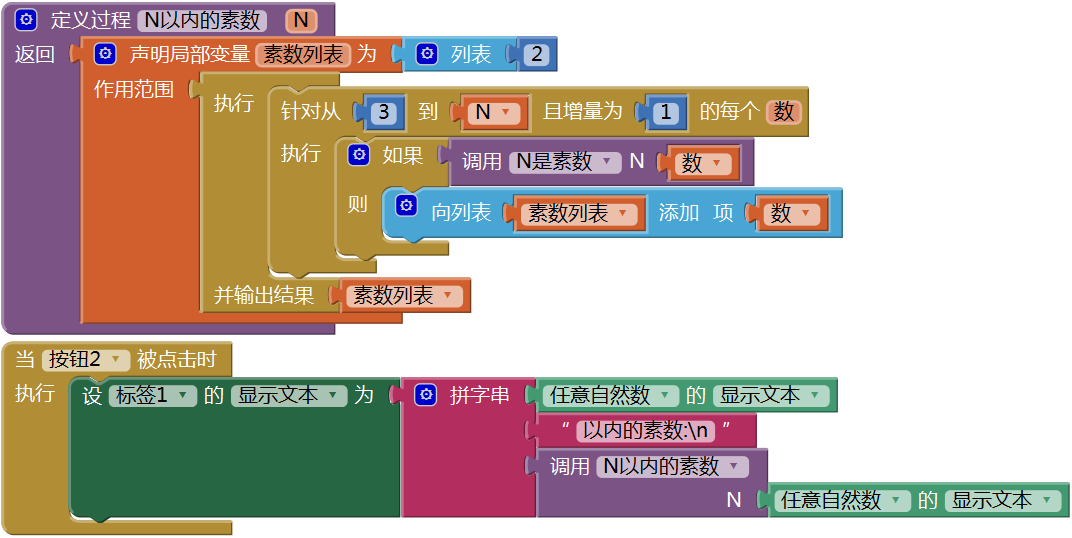 图15-17 求N以内的全部素数
图15-17 求N以内的全部素数 图15-18 求N以内素数的测试结果
图15-18 求N以内素数的测试结果 四、改造N是素数过程
声明一个全局变量——N以内素数,将“N以内的素数”过程的返回值保存到该全局变量中,这个运算结果可以帮助我们提高判断素数程序的运行效率,代码如图15- 19所示。
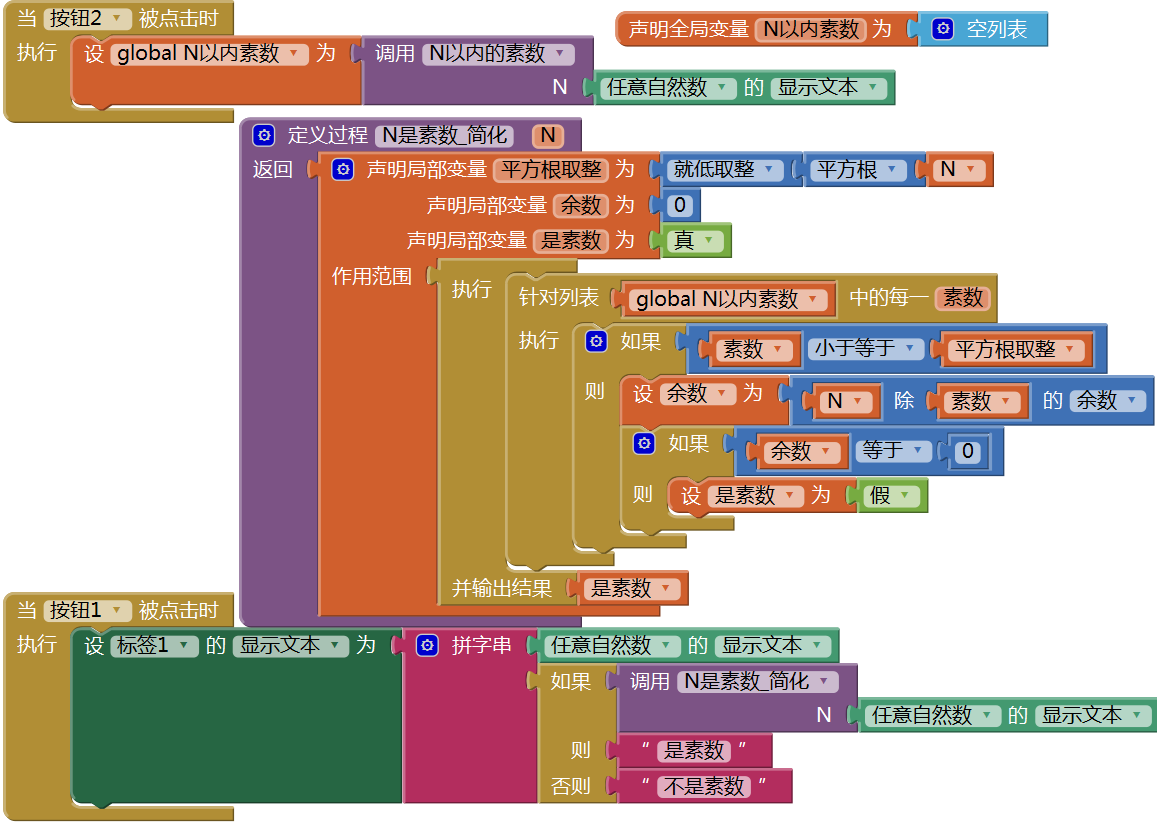 图15-19 利用已经获得的N以内素数列表,改进对素数的判断程序
图15-19 利用已经获得的N以内素数列表,改进对素数的判断程序图中“N是素数_简化”过程中,利用针对列表的循环,对全局变量“N以内素数”列表进行遍历,以便进一步减少循环次数。仍以33133为例,从图15- 18中可知,182以内共有42个素数,因此,实际上程序仅对42个素数进行了求余数运算。
上述程序中还有进一步改进的空间,例如,针对N以内素数的循环,如果能改为针对182以内素数的循环,则循环次数还可以降低,或者,将针对列表的循环改为“满足条件循环”,也可以减少循环次数。
以上我们讨论了对素数的判断,以及如何求N以内的素数,下一节我们将在此基础上讨论素数的应用——如何求两个自然数的最大公约数及最小公倍数。
第四节 求M与N的最大公约数
一、概念陈述
- 约数:有整数P、N,如果N能被P整除,则称P是N的约数。例如100能被25整除,则25称为100的约数;100的约数包括2、4、5、10、20、25及50,共7个。
- 公约数:有整数P、M、N,如果M、N都能被P整除,则称P是M、N的公约数。例如,75的约数为:3、5及25,则100与75的公约数为5及25。
- 最大公约数:整数M、N的所有公约数中,最大的公约数称为最大公约数。例如,75与100的最大公约数为25。
二、概念的数学表示
- 约数:针对整数N,如果仅能被1及其自身整除,则N为素数,否则,N为合数。对于合数N,可以分解为若干个质因数的乘积。例如100=2x25x5,150=235x5,300=2x235x5,等等。注意,这里用“x”表示相同质因数之间的乘法,用“”表示不同质因数之间的乘法,这两种表示方法只是符号不同,它们的作用完全相同,下同。
- 公约数:整数M、N的约数中共同的部分。例如100与150的公约数为2、5及5x5,100与300的公约数为2、2x2、5及5x5,150与300的公约数为2、3、5及5x5。
- 最大公约数:整数M、N的公约数中的最大值。例如100与150的最大公约数是50(25x5), 100与300的最大公约数为100(2x25x5),150与300的最大公约数为150(235x5)。
从上述最大公约数的表示方法中不难发现,M、N的最大公约数等于它们质因数乘积中共有的部分。为了更清楚地表达这一结果,我们需要借用乘方的概念(小学的读者们可以请求家长的帮助):一个合数M可以分解为若干个质因数乘方的乘积,其中乘方的底数为质因数,乘方的指数为该质因数在分解结果中的个数。例如100=2252,150=2352,300=223*52。如果想求得两个数的最大公约数,首先需要找到两者的分解结果中的共同质因数,作为乘方的底数,设它们为P1、P2、…Pn;然后查看分解结果中P1、P2…Pn的个数,并找到各自的最小个数m1、m2、…mn,作为乘方的指数,最后,最大公约数可以表示为:
P=P1m1*P2m2*…*Pnmn (读作P1的m1次方乘以P2的m2次方乘以…乘以Pn的mn次方)
下面举例说明上述表示法,仍然以150与300为例,它们的分解结果中均包含质因数2、3、5,以质因数2为例,在150中包含1个2(2的1次方),在300中包含2个2(2的2次方),则最大公约数中保留1个2(2的1次方),因此它们的最大公约数为213152。
有了上述结论,我们可以用代码来表示两个整数的质因数,并求得它们的最大公约数。
三、概念的程序表示
(1) 求约数:将整数N分解为质因数乘方的乘积,并将乘方的底数与指数保存到列表中。以150与300为例,将它们的分解结果保存在列表中,如图15- 20所示。
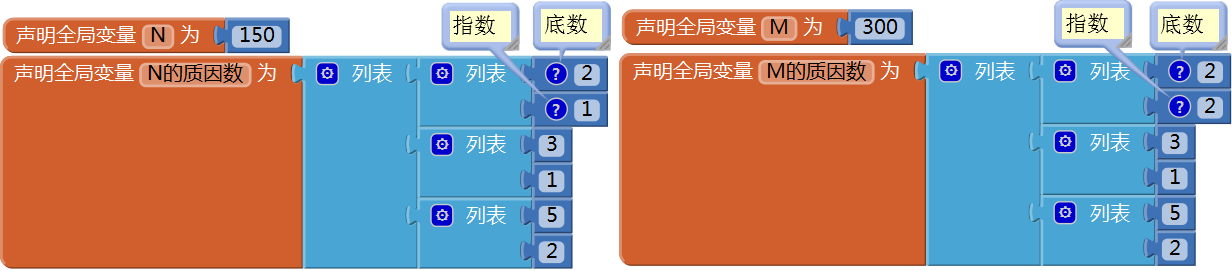 图15-20 合数M与N的列表表示
图15-20 合数M与N的列表表示图中的列表为二级列表,一级列表的长度等于质因数的个数,二级列表的长度为2,其中第一项为质因数——乘方的底数,第二项为该质因数的个数——乘方的指数。
(2) 求最大公约数 先来编写一个有返回值的过程——最大公约数,暂时不考虑过程的通用性,就以图15- 20中的数据为例,来求得150与300的最大公约数,代码如图15- 21所示。
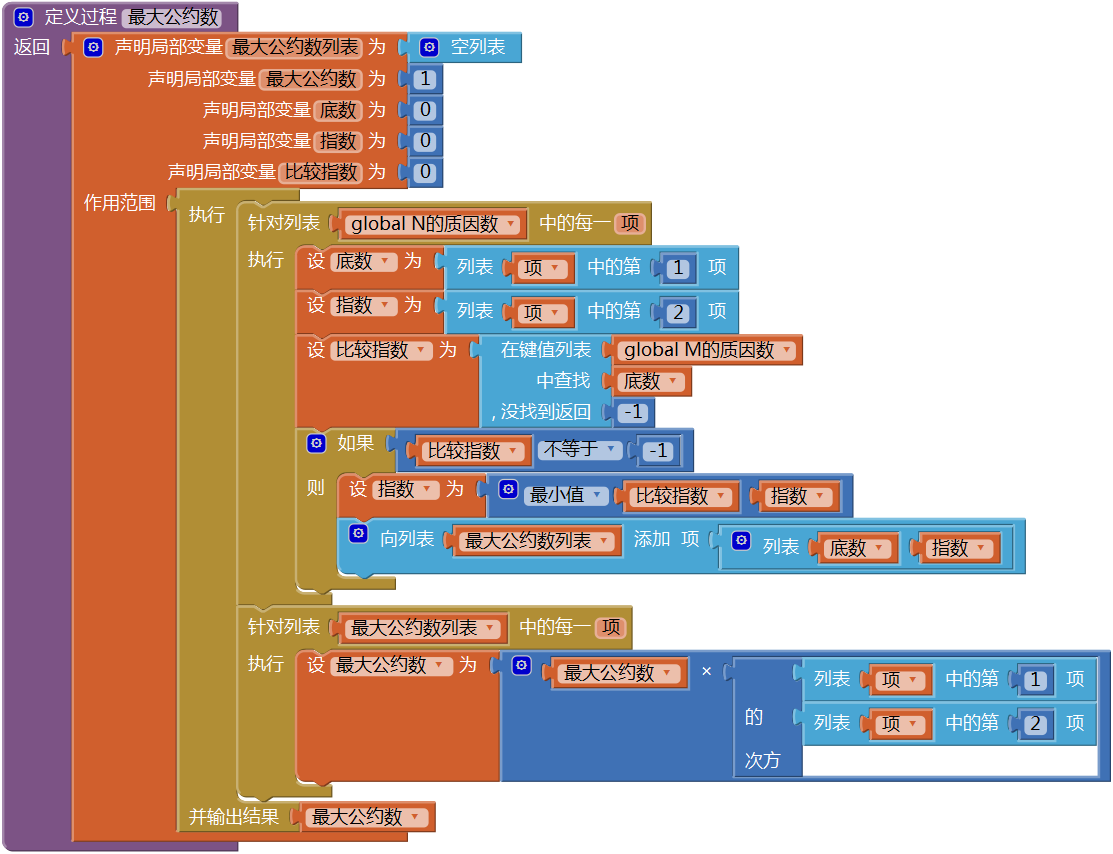 图15-21 求最大公约数的过程
图15-21 求最大公约数的过程代码中包含两个针对列表的循环语句,第一个循环语句对“N的质因数”列表进行遍历,其中的循环变量“项”为列表,包含2个列表项,分别为质因数(底数)及质因数的个数(指数)。在循环开始时,首先求得底数及指数值,利用底数作为“键”,在键值对列表“M的质因数”中进行查找;如果“M的质因数”列表中包含被查找的“键”,则返回值为该底数的个数,否则返回“-1”;无论返回值是否为-1,都将返回结果保存到局部变量“比较指数”中;如果“比较指数”不等于-1,则将“指数”与“比较指数”中值较小的设定为最终的“指数”值,并将这一组“底数”与“指数”添加到局部变量“最大公约数列表”中。
当完成对“N的质因数”列表的遍历后,执行第二个针对列表的循环语句——计算最大公约数的值,最后将最大公约数的值返回给过程的调用者。
为了测试上述代码的执行结果,我们在屏幕初始化程序中,调用“最大公约数”过程,并利用屏幕的标题属性来显示程序的执行结果,代码如图15- 22所示,测试结果如图15- 23所示。
 图15-22 利用屏幕的标题来显示程序的运行结果
图15-22 利用屏幕的标题来显示程序的运行结果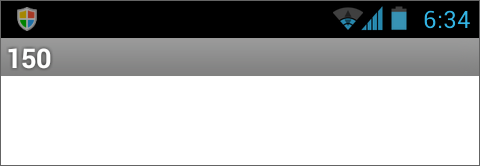 图15-23 求最大公约数的测试结果
图15-23 求最大公约数的测试结果以上我们仅以150及300两个整数为例,演示了求两个整数最大公约数的方法:首先演示了数学方法:将两个整数分解为若干个质因数乘方的乘积,并从分解结果中提取两者共有的部分,作为两个整数的最大公约数;其次,在App Inventor中,利用列表数据保存两个整数的分解结果,并利用针对列表的循环语句,查找分解结果中共有的部分,最终计算出两个整数的最大公约数,并显示在屏幕的标题中。
上述程序只是针对两个具体的数字,而且已经手工将它们分解为质因数乘方的乘积,讨论的内容并没有涉及到如何将整数分解为质因数乘方之积,并保存到列表中。下面我们创建一个项目——最大公约数与最小公倍数,并添加简单的组件,来实现完整的功能——求两个任意整数的最大公约数。
四、求任意两个整数的最大公约数
1、用户界面设计
对于数学类的应用,我们强调的是解决问题的思路,以及将数学问题转化为程序问题的方法,因此对于用户界面设计,只求能够显示运算结果。如图15- 24所示,在新建的项目中,添加两个文本输入框,分别命名为M及N,勾选其“仅限数字”属性;添加一个水平布局组件,将两个按钮添加到水平布局组件中,分别命名为“公约数按钮”及“公倍数按钮”;添加一个标签,命名为“结果”,用于显示程序的运行结果。
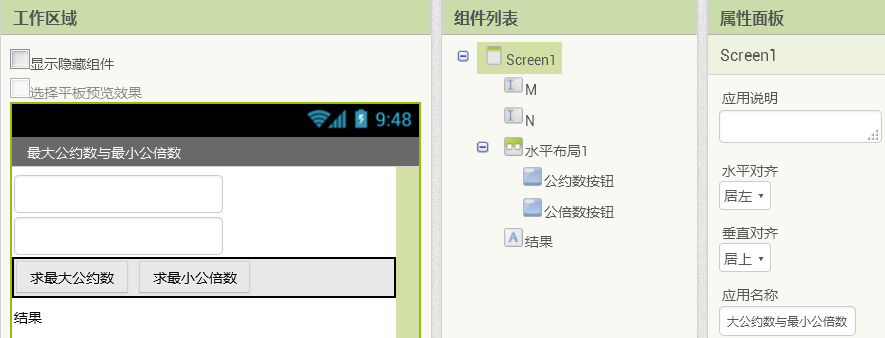 图15-24 求最大公约数与最小公倍数的用户界面
图15-24 求最大公约数与最小公倍数的用户界面2、编写过程——分解整数
在上一节我们创建了两个有返回值的过程——“N是素数”及“N以内的素数”,本节将利用这些结果来分解整数,将任意整数分解为若干质因数乘方的乘积。
(1) 打开“素数求解”项目,将上述两个过程及全局变量“N以内素数”放置到代码块背包中,回到“最大公约数与最小公倍数”项目中,将上述代码块从背包中提取出来;
(2) 在屏幕初始化程序中,调用“N以内的素数”过程,并将过程返回值保存到全局变量“N以内素数”中,代码及测试结果如图15- 25所示;
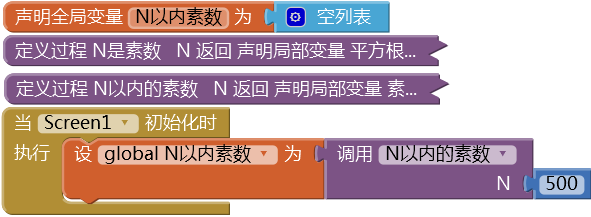 图15-25 在屏幕初始化时,求500以内的素数
图15-25 在屏幕初始化时,求500以内的素数(3) 创建一个有返回值过程——素数实用集。对于任意整数N,它的最大质因数不可能大于N,因此,当我们将N分解为若干质因数乘方之积时,只需要针对那些小于等于N的素数进行筛选。为此,我们对全局变量“N以内素数”进行遍历,以便获得满足需要的最小素数集合,具体代码如图15- 26所示。
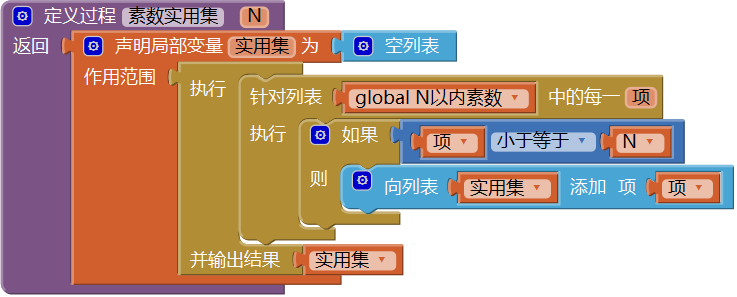 图15-26 过程——素数实用集
图15-26 过程——素数实用集(4) 创建一个有返回值过程——质因数。对于任意给定的整数N(被除数),判断某个素数P(除数)是否为它的质因数(P能整除N),如果是,则求出整数N中包含的P的个数(N能够被P整除的次数)。该过程的返回值为列表,包含两个列表项,第一个列表项为素数P(除数),第二个列表项为N被P整除的次数,具体代码如图15- 27所示。
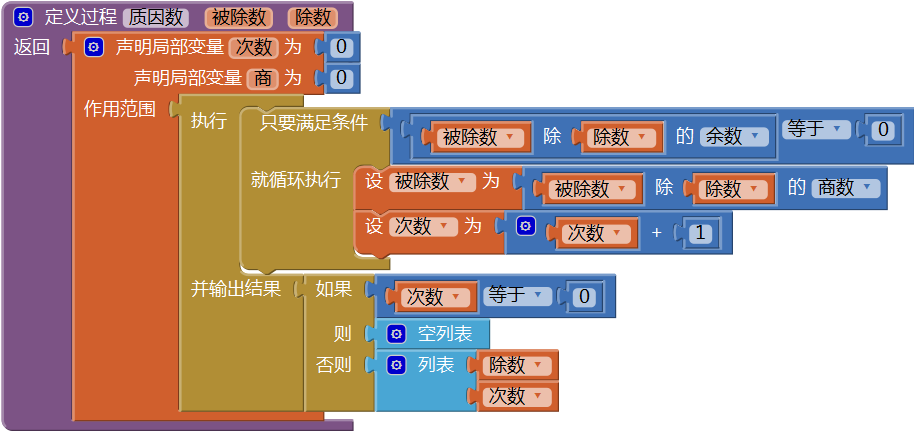 图15-27 过程——质因数
图15-27 过程——质因数(5) 创建一个有返回值过程——质因数列表。对于任意给定的整数N,遍历它的素数实用集列表,通过调用“质因数”过程,可以筛选出它的全部质因数(包括质因数本身以及被整除的次数)。该过程的返回值为二级列表,列表结构与图15- 20中“N的质因数”相同,具体代码如图15- 28所示。
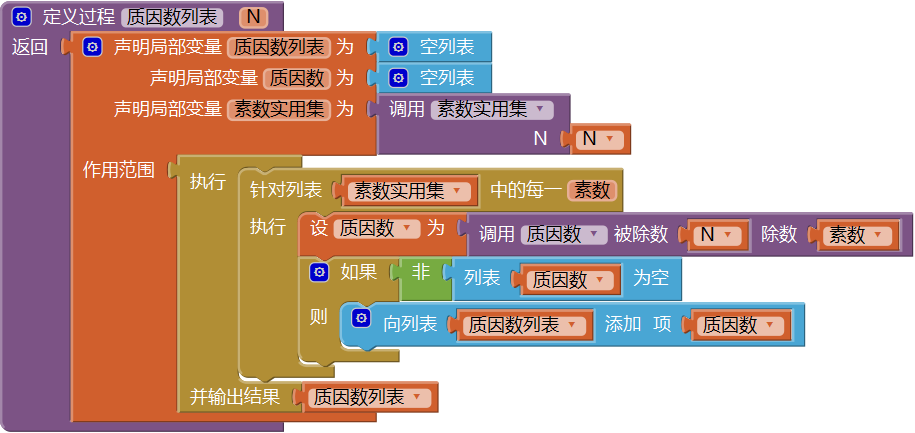 图15-28 过程——质因数列表
图15-28 过程——质因数列表利用公约数按钮的点击程序对上述过程进行测试,代码如图15- 29所示。测试结果如图15- 30所示。
 图15-29 在结果标签中显示质因数列表
图15-29 在结果标签中显示质因数列表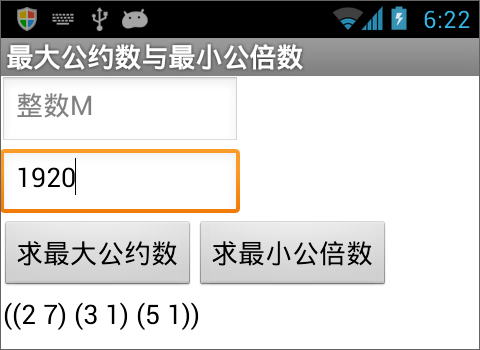 图15-30 测试——求整数1920的质因数列表
图15-30 测试——求整数1920的质因数列表(6) 改造过程——最大公约数。在图15- 21的“最大公约数”过程里,我们利用两个全局变量“M的质因数”与“N的质因数”,求得了150与300的最大公约数,现在我们要对该过程进行改造,将全局变量替换为过程的参数“M质因数列表”与“N质因数列表”,以便该过程可以求取任意两个质因数列表的最大公约数。修改后的代码如图15- 31所示。
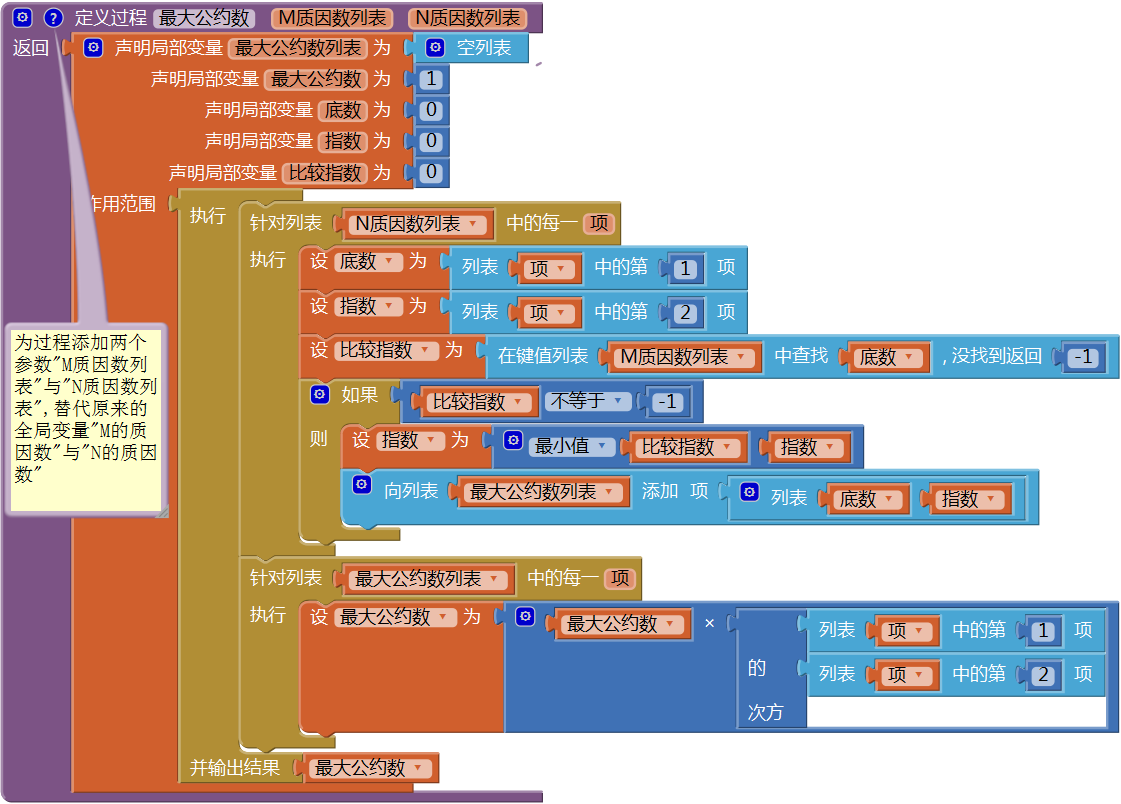 图15-31 改造之后的最大公约数过程
图15-31 改造之后的最大公约数过程(7) 公约数按钮点击程序——用“结果”标签显示“最大公约数”过程的返回值。在“最大公约数”过程里两次调用“质因数列表”过程,分别将用户输入的两个整数作为参数,求取两个整数的质因数列表,并最终求得两个整数的最大公约数,代码如图15- 32所示。
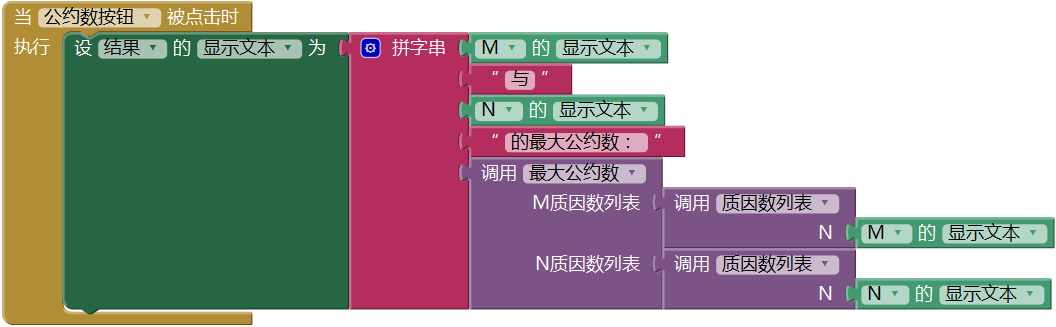 图15-32 在公约数按钮的点击程序中调用“最大公约数”过程
图15-32 在公约数按钮的点击程序中调用“最大公约数”过程(8) 测试——在用户界面上输入不同的整数,求取它们的最大公约数,测试结果如图15- 33所示。建议读者自己用纸笔计算一下图中的题目,来验证一个图中的结论是否正确。
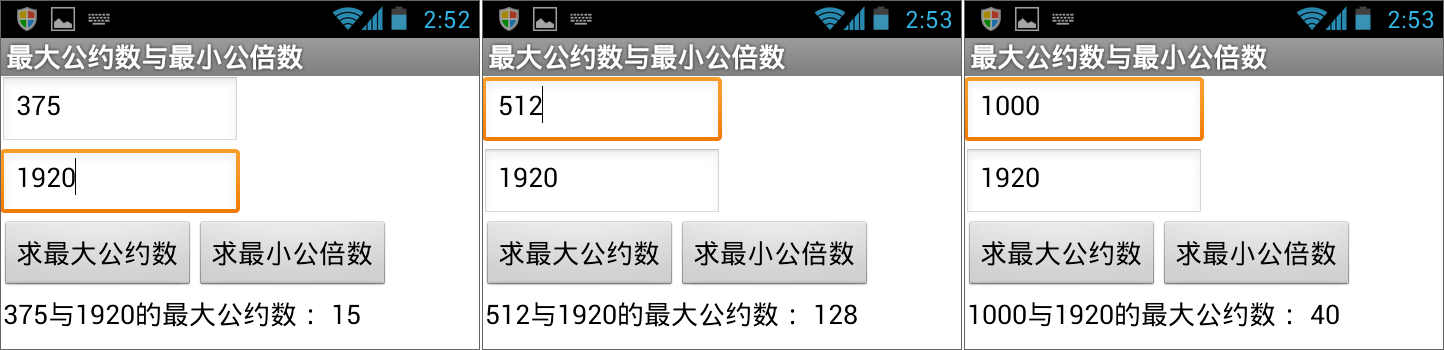 图15-33 测试——求任意两个整数的最大公约数
图15-33 测试——求任意两个整数的最大公约数以上我们实现了求取两个整数最大公约数的目标,在这个过程中,有两个关键步骤:
- 将实际问题转化为数学问题——用数学语言描述问题的本质:将整数分解为质因数乘方之积,并明确两个整数的最大公约数就是它们分解结果中共有的部分;
- 将数学问题转化为程序问题——用列表表示对整数的分解结果,利用循环语句筛选出分解结果中共有的部分, 并计算出最终的结果。
下面我们来解决本章的最后一个问题——求两个整数的最小公倍数。
第五节 求M与N的最小公倍数
一、问题的数学表示
有了前面求最大公约数的经验,求最小公倍数的问题变得简单了。解决问题的起点是对两个整数进行质因数分解的结果。仍然以100及150为例,100=2252,150=2352,最大公约数是这两个结果中共有的部分(252=50),而最小公倍数则是两个结果中能够包含两个结果的最小集合(22352=300),我们把这个最小集合称为“结果集”。这里面有两重含义:
- 结果集中包含两个整数的全部质因数,例如,100与150的结果集中包含2、3、5三个质因数;
- 每个质因数乘方的指数取两个分解结果中的最大值,例如100与150中都包含质因数2,100中包含2的2次方,150中包含2的1次方,则结果集中保留较大者,即2的2次方。
有了上述结论,接下来我们把数学问题转换为程序问题。
二、问题的程序表示
1、合并两个整数的质因数列表
解决问题的起点是两个整数的质因数列表——“质因数列表”过程的返回值。我们创建一个过程——最小公倍数列表,对两个质因数列表进行合并,代码如图15- 34所示。
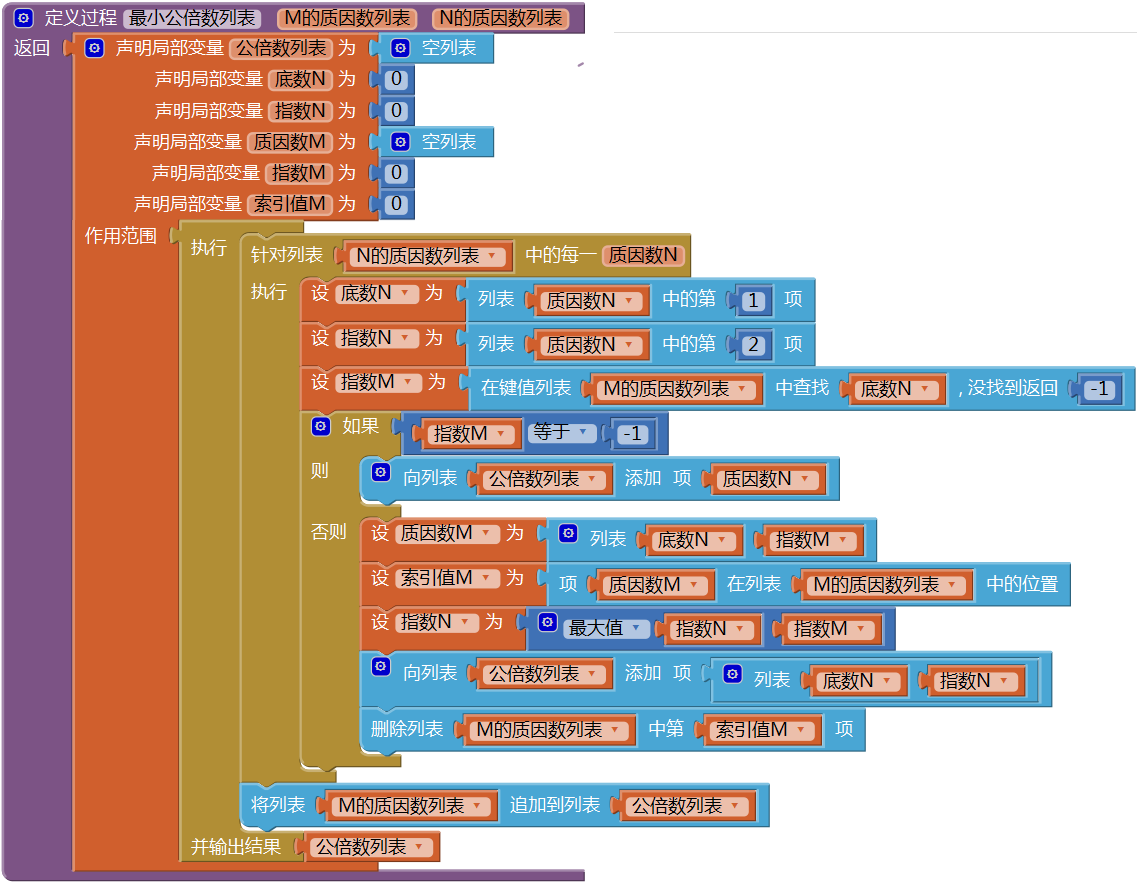 图15-34 过程——最小公倍数列表
图15-34 过程——最小公倍数列表仍然沿用求最大公约数列表的思路,对N的质因数列表进行遍历。对于每一个N的质因数,在M的质因数列表中查找是否存在相同的质因数(底数),如果不存在,则指数M=-1,此时,将正在接受遍历的质因数N添加到公倍数列表中;如果存在,则首先取得“质因数M”在“M的质因数列表”中的索引值,并设指数N为两个指数中的最大值,将底数N与指数N组成的列表添加到公倍数列表中,并将“质因数M”从“M的质因数列表”中删除。当对“N的质因数列表”的遍历完成时,该列表中的全部列表项已经被添加到公倍数列表中,其中有些质因数的指数可能被改写为更大的值(M的质因数列表中对应底数的指数值),而M的质因数列表中的重复项已经被删除干净,剩下的列表项被一次性地追加到公倍数列表中。最后,将公倍数列表返回给调用者。
2、求最小公倍数
对最小公倍数列表进行遍历,求得所有质因数乘方的乘积,代码如图15- 35所示。
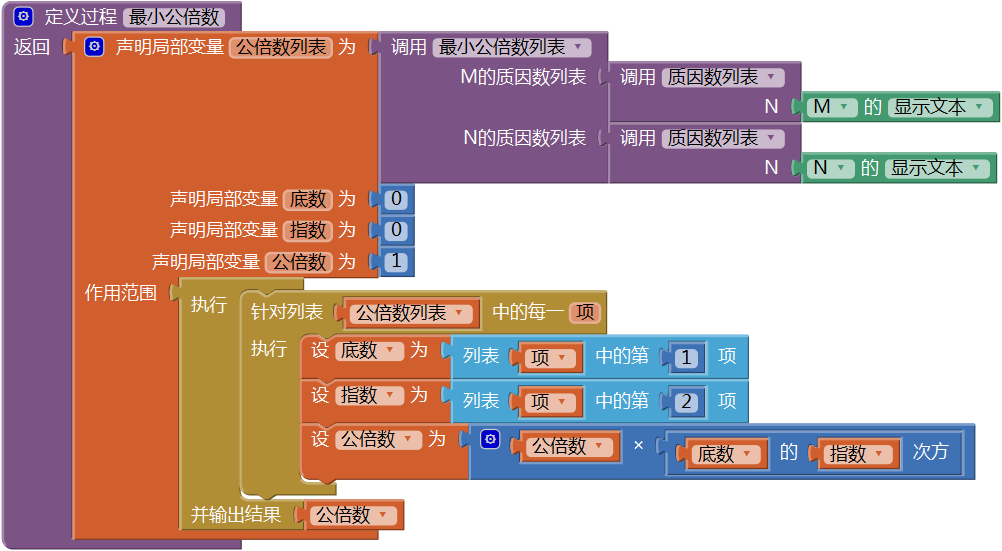 图15-35 过程——最小公倍数
图15-35 过程——最小公倍数3、显示运算结果
在公倍数按钮的点击程序中,调用最小公倍数过程,并将运算结果显示在“结果”标签中,代码如图15- 36所示。
 图15-36 显示最小公倍数的运算结果
图15-36 显示最小公倍数的运算结果4、测试
如图15- 37所示,在文本输入框M及N中分别输入不同的数字,“结果”标签中显示了最小公倍数的运算结果。
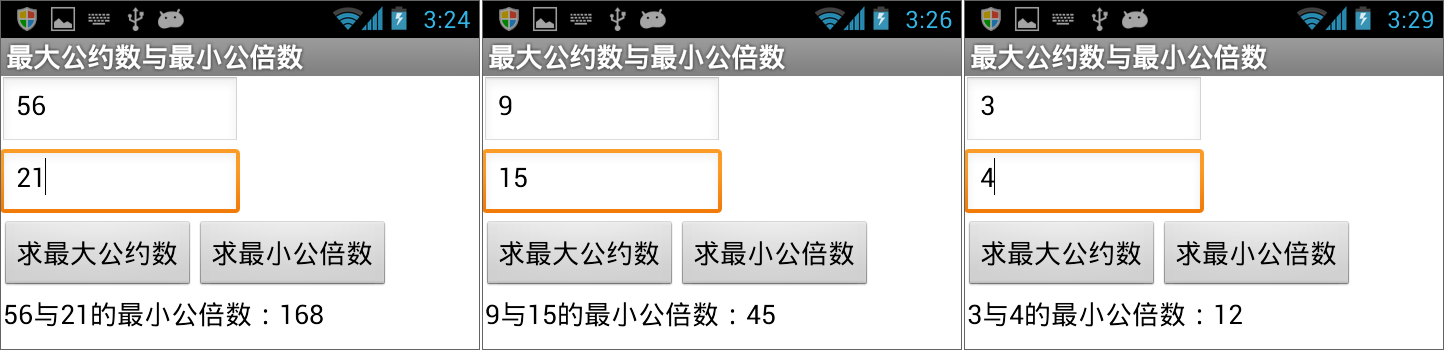 图15-37 测试——显示最小公倍数的运算结果
图15-37 测试——显示最小公倍数的运算结果第六节 小结
作为“数学实验室”的第一部分,我们对几个常见的数学问题进行了讨论,从简单的鸡兔同笼,到素数求解,再到稍微复杂一些的公约数、公倍数问题。这些内容基本上属于小学数学的范围(乘方除外),大多数人都会用数学方法解决这些问题,但是,如何将简单的数学问题转化为程序问题,却是需要我们从惯性思维中摆脱出来,让自己的思维“慢”一点,并且“笨”一点。
所谓“慢”一点,就是将时间放大,再放大,捕捉自己思考过程中留下的每一丝线索,将它们记录下来。这些思考的线索,就像风中的一丝花香,稍纵即逝,需要安静与专注,才能有所收获。
所谓“笨”一点,就是回归我们的天真状态,忘记那些高级的技巧,以最质朴的方法去面对问题,并解决问题。之所以要“笨”一点,是因为计算机并不像你想象的那样无所不能,相反,它其实比人类“笨”的太多太多,因此,用计算机解决问题,你就要向它“靠拢”,习惯于它的逻辑和方法,只有这样,才能找到解决问题的钥匙。